MARZO TEMAS: 4.2 y 4.3

TEMAS:

4.2. Aplicar el teorema de Pitágoras en la resolución de problemas.

4.3. Reconocer y determinar las razones trigonométricas en familias de triángulos rectángulos semejantes, como cocientes entre las medidas de los lados. Calcular medidas de lados y de ángulos de triángulos rectángulos a partir de los valores de razones trigonométricas.

TEOREMA DE PITAGORAS:

El Teorema de Pitágoras establece que en un triangulo rectangulo, el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual, a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se establece que:

RAZONES TRIGONOMETRICAS EN TRIANGULOS :

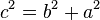
Las funciones trigonométricas, en matematicas, son relaciones angulares; guardan relación con el estudio de la geometria de los triangulos y son de gran importancia en astronomia,cartografia, nautica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.
La función Seno se obtiene de dividir el cateto opuesto de un triángulo rectángulo, entre su hipotenusa.

Función Cosecante
La función cosecante es parecida a la función seno, sólo que al revés. Esto es: en lugar de dividir el cateto opuesto entre la hipotenusa, se divide la hipotenusa entre el cateto opuesto

Función Coseno:
La función Coseno se obtiene de dividir el cateto adyacente de un triángulo rectángulo, entre su hipotenusa.

Función Secante
La función secante es parecida a la función coseno, sólo que al revés. Esto es: en lugar de dividir el cateto adyacente entre la hipotenusa, se divide la hipotenusa entre el cateto adyacente.

Función Tangente:
La función Tangente se obtiene de dividir el cateto opuesto de un triángulo rectángulo, entre el cateto adyacente:
Así por ejemplo, en el triángulo rectángulo siguiente:
la tangente del ángulo alpha será:
Para obtener el valor de ángulo alpha, hay que sacar la función inversa de la tangente:
cualquier calculadora científica lo puede hacer, y generalmente hay que apretar una tecla "shift" o "2daf" que se encuentra típicamente en la esquina superior izquierda, y luego apretar la tecla "tan":
para este caso, el resultado da: 53.13010...
que es el valor en decimal que corresponde al ángulo alpha.
La función tangente se puede también definir a través de las funciones seno y coseno como sigue:
y el resultado es el mismitito que dividir el cateto opuesto entre el cateto adyacente.

Función Cotangente
La función cotangente es parecida a la función tangente, sólo que al revés. Esto es: en lugar de dividir el cateto opuesto entre el cateto adyacente, se divide el cateto adyacente entre el cateto opuesto
hay otras notaciones válidas para la contangente, algunos la prefieren escribir de alguna de las siguientes formas:
pero es la misma función.

FEBRERO TEMAS: 3.4 y 3.5

TEMAS:

3.4. Determinar los resultados de una homotecia cuando la razón es igual, menor o mayor que 1 o que –1. Determinar propiedades Invariantes al aplicar una homotecia. Comprobar que una composición de homotecias con el mismo centro es igual al producto de las razones.

3.5. Gráficas de relaciones funcionales no lineales.

HOMOTECIA:

Una homotecia es una trasformación geométrica que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. Es una amplificación. Su definición rigurosa es vectorial:

Definición

Sea E un espacio vectoral sobre un cuerpo K. Sea Ω un elemento (visto como un punto) de E

La homotecia de centro Ω y de razón k, denotada h_{Ω, k} envía un punto M del espacio vectorial sobre el punto M' tal que:

GRAFICAS EN RELACIONES NO LINEALES:


Las funciones no lineales no tienen tasas de cambio constantes. Por lo tanto, sus gráficas no son líneas rectas.

ENERO TEMAS: 3.2 y 3.3

TEMAS:

3.2. Utilizar ecuaciones cuadráticas para modelar situaciones y resolverlas usando la fórmula general.

3.3. Determinar el teorema de Ta

les mediante construcciones con segmentos. Aplicar el teorema de Tales en diversos problemas

geométricos.

ECUACIONES CUADRATICAS:

Es un tipo de ecuación particular en la cual la variable o incógnita está elevada al cuadrado, es decir, es de segundo grado. Un ejemplo sería: 2X² - 3X = 9. En este tipo de ecuación no es posible despejar fácilm ente la X, por lo tanto se requiere un procedimiento general para hallar las soluciones.
l procedimiento consiste en realizar modificaciones algebraicas en la ecuación general de la ecuación de segundo grado: ax2+bx+c = 0 hasta que la X quede despejada. Dicho procedimiento no será cubierto en este documento. La solución de una ecuación de segundo grado es la llamada FORMULA RESOLVENTE.

La fórmula genera dos respuestas: Una con e

l signo + y otra con el signo - antes de la raíz. Solucionar una ecuación de segundo grado se limita entonces, a identificar las letras a,b y c y sustituir sus valores en la fórmula resolvente.

Es de hacer notar que, utilizar la fórmula resolvente es un procedimiento que debe realizarse con cuidado y requiere extraer la raíz cuadrada de un número, bien sea con calculadora o cualquier proce

so manual.

Estas dificultades hacen que el estudiante inexperto se equivoque constantemente en la solución. Existen procedimientos particulares, sólo aplicables a ciertos casos, en los cuales se pueden hallar las raíces de forma mas fácil y rápida. Tienen que ver con las técnica

s de factorización.

TEOREMA DE TALES:

El teorema de Tales demuestra la relación de proporcionalidad entre los segmentos que delimitan rectas secantes sobre rectas paralelas. Es muy útil para dividir un segmento en partes iguales o proporc

ionales a otros segmentos.

DICIEMBRE TEMAS: 2.4 Y 2.5

TEMAS:

2.4. Aplicar la semejanza de triángulos en el cálculo de distancias o alturas inaccesibles.

2.5. Interpretar y utilizar índices para explicar el comportamiento de diversas situaciones.

FIGURAS SEMEJANTES:

Dos triángulos son semejantes si tienen la misma forma. En tal caso cumplen que:

Una semejanza es la composición de una materia (una rotación y una posible reflexión o simetría axial) con una homotecia.En la rotación se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma.

Por lo tanto, dos triángulos son semejantes si tienen similar forma.

En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de unrectángulo, por ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura).

Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos.

En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con D, E y F, respectivamente.

INDICES PARA EXPLICAR EL COMPORTAMIENTO DE DIVERSAS SITUACIONES:

NOVIEMBRE TEMAS: 2.1 Y 2.2

TEMAS:

2.1. Utilizar ecuaciones no lineales para modelar situaciones y resolverlas utilizando Procedimientos personales u operaciones inversas.

2.2. Utilizar ecuaciones cuadráticas para modelar situaciones y resolverlas usando la factorización.

ECUACIONESNO LINEALES:

Las ecuaciones diferenciales No-Lineales son una tecnica derivada de un concepto mucho mas general el cual son las ecucaciones diferenciales, pero aun cuando un tema es derivado deel otro, existen diferencia entre estos al momento de la aplicacion, por ejemplo, las ecucaciones diferenciales no lineales de primero orden pueden tener soluciones singulares, mientrasn que las ecuaciones no lineales, no.

Los sistemas no lineales representan sistemas cuyo comportamiento no es expresable como la suma de los comportamientos de sus descriptores.

Una ecucacion no lineal es una ecuacion de la forma:

F(u)=0, para algun valor desconocido de u. para poder resolver cualquier ecuacion se necesita decidir en que espacio matematico se encuentra la solucion u , podria ser que uu es un numero real.

ECUACIONES CUADRATICAS:

es una ecuación de la forma ax2 + bx + c = 0 donde a, b, y , c son números reales y a es un número diferente de cero.

Ejemplo:
9x2 + 6x + 10 a = 9, b = 6, c = 10
3x2 - 9x a = 3, b = -9, c = 0
-6x 2 + 10 a = -6, b = 0, c = 10

La condición de que a es un número diferente de cero en la definición asegura que exista el término x2 en la ecuación. Existen varios métodos para resolver las ecuaciones cuadráticas. El método apropiado para resolver una ecuación cuadrática depende del tipo de ecuación cuadrática que se va a resolver. En este curso estudiaremos los siguientes métodos: factorización, raíz cuadrada, completando el cuadrado y la fórmula cuadrática.

Hay tres formas de hallar las raíces ( el o los valores de la variable) de las ecuaciones cuadráticas:
1. Factorización Simple 2. Completando el Cuadrado 3. Fórmula Cuadrática

Factorización Simple:
La factorización simple consiste en convertir la ecuación cuadrática en un producto de binomios. Luego, se busca el valor de x de cada binomio.

Ejemplo: Realizar la factorización simple de la ecuación
x2 + 2x – 8 = 0 a = 1 b = 2 c = - 8
(x ) (x ) = 0 [x ·x = x2]
( x + ) (x - ) = 0

Completando el Cuadrado:
En este método, la ecuación tiene que estar en su forma ax2+bx+c; y siempre la constante de a tiene que ser igual a 1. Por ejemplo, para factorizar la ecuación 4x2 + 12x – 8 = 0, hay que despejar de la siguiente forma:
4x2 + 12x – 8 = 0 4 4 4 4

x2 + 3x – 2 = 0 Ahora, a= 1.

Fórmula Cuadrática:
Este método es muy simple: hay que sustituir los valores de a, b y c de la ecuación cuadrática a la siguiente fórmula:
Ejemplo:
X2 + 2x – 8 = 0 a = 1, b = 2, c = -8

OCTUBRE TEMAS : 1.5 Y 1.6

TEMAS:


1.5. Calcular la medida de ángulos inscritos y centrales, así como de arcos, el área de sectores circulares y de la corona.

1.6. Analizar la razón de cambio de un proceso o fenómeno que se modela con una función lineal y
relacionarla con la inclinación o pendiente de la recta que lo representa.



ANGULO INSCRITO:






En geometría, un ángulo inscrito es el ángulo comprendido entre dos secantes (o una secante y una tangente en el caso degenerado, llamado semi-inscrito), que se intersecan en la circunferencia. Es decir, es el ángulo definido por dos cuerdas que comparten un extremo.

ANGULO CENTRAL:

Es un ángulo cuyos lados son radios y su vértice es el centro de la circunferencia.
Es la referencia fundamental para los otros tipos de ángulos en el círculo (inscrito, interior, exterior) pues la medida del ángulo central es proporcional (con constante ) a su arco interceptado. Ver definición de radián.




RAZON DE CAMBIO :

cuando el cambio que experimenta una magnitud afecta a otra, se dice ue entre ambas magnitudes existe una relacion llamada razon de cambio. La pendiente es una razon de cambio que describe la inclinacion de la recta en el plano carteciano.

SEPTIEMBRE TEMAS: 1.3 Y 1.4

TEMA:

1.3. Caracterizar la recta secante y la tangente a unacircunferencia.

1.4. Determinar la relación entre un ángulo inscrito y un ángulo central de una circunferencia, si ambosabarcan el mismo arco.

RECTAS Y SEGMENTOS NOTABLES EN LA CIRCUNFERENCIA:

Secante: recta que corta a la circunferencia en dos puntos.

Tangente: recta que corta a la circunferencia en un solo punto.

Rectas tangentes a dos circunferencias

Dos circunferencias C y C' poseen, en general, cuatro rectas tangentes comunes. Dichas tangentes, así como los respectivos puntos de tangencia, son simétricas dos a dos respecto de la recta CC' que une los centros de las circunferencias. Cada par de tangentes simétricas se cortan en un punto de la recta CC'. En función de la ubicación de este punto se distingue entre tangentes interiores (cuando el punto de corte está situado entre los dos centros C y C') y tangentes exteriores (en el caso contrario) a las dos circunferencias. Estos puntos de corte de las tangentes simétricas no son otros que los centros de homotecia positiva y negativa de las circunferencias.